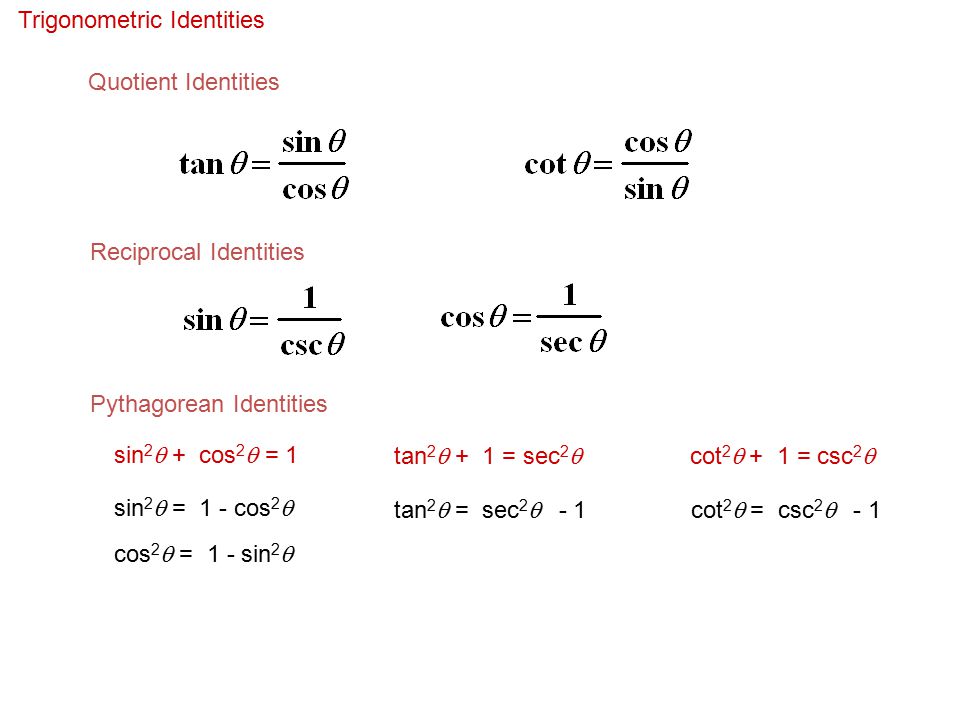
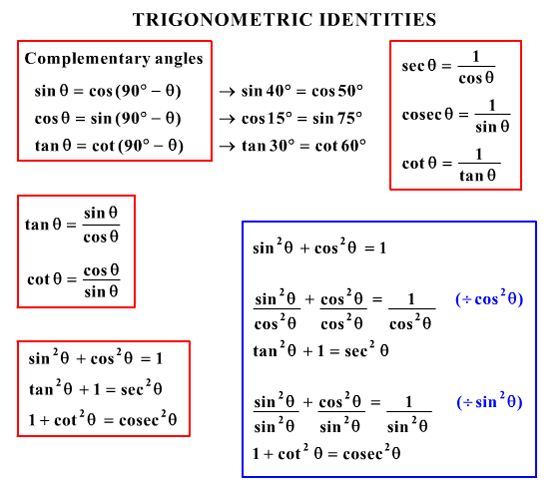
The Pythagorean identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan( − θ) = − tanθ cot( − θ) = − cotθThe basic trigonometric functions include the following \(6\) functions sine \(\left(\sin x\right),\) cosine \(\left(\cos x\right),\) tangent \(\left(\tan x\rightHyperbolic Trig Identities is like trigonometric identities yet may contrast to it in specific terms The fundamental hyperbolic functions are hyperbola sin and hyperbola cosine from which the other trigonometric functions are inferred You can easily explore many other Trig Identities on this website So here we have given a Hyperbola diagram along these lines giving you thought

Ch 7 Trigonometric Identities And Equations Ppt Video Online Download
Trigonometric identities tan^2x
Trigonometric identities tan^2x- We will apply the following more fundamental trigonometric identity $\boxed{\tan^2 x 1 = \sec^2 x}$ The proof is started from the righthand side Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity Trigonometry




Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com
In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = \\frac{2\text{tan x}}{1 tan^{2}x}\Didn't find what you were looking for?
Proving trig identity $\tan(2x)−\tan(x)=\frac{\tan(x)}{\cos(2x)}$ Ask Question Asked 4 years, 1 month ago Active 4 years, 1 month ago Viewed 4k times 1 1 $\begingroup$ I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫ (1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) CTrigonometric identities are equations that relate different trigonometric functions and are true for any value of the variable that is there in the domainBasically, an identity is an equation that holds true for all the values of the variable(s) present in it
TRIGONOMETRIC IDENTITIES RECIPROCAL IDENTITIES PYTHAGOREAN = x SUM AND sin x sin tan ± y DOUBLEANGLE IDENTITIES 2x = 2 = = x — X — tan x tan = HAL F ANGLE sin tanDouble or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x = 3 sin x – 4 sin³x 5) cos3x = 4 cos³x – 3 cosx 6) tan 3x = (3 tan x – tan³x) / (1 3tan²x) Sum and difference formulas of different trigonometric functions are asIf the power of the secant \(n\) is odd, and the power of the tangent \(m\) is even, then the tangent is expressed in terms of the secant using the identity \(1 {\tan ^2}x \) \(= {\sec ^2}x\) After this substitution, you can calculate the integrals of the secant




Math34 Trigonometric Formulas




Which Of The Following Equations Are Identities Check All That Apply A Cot 2x Csc2x 1 B Brainly Com
Then use the substitution = (), also use the Pythagorean trigonometric identity 1 − sin 2 arctan ( x ) = 1 tan 2 arctan ( x ) 1 {\displaystyle 1\sin ^{2}\arctan(x)={\frac {1}{\tan ^{2}\arctan(x)1}}}And the Pythagorean identity cos2 x sin2 x= 1 we nd cosx tanxsinx=cosx sinx cosx sinx = cos 2x sin x cosx = 1 cosx = secx Establishing Trigonometric Identities A trigonometric identity is a trigonometric equation that is valid for all values of the variable for which the expressions in the equation are de ned How2 x – 1 Third doubleangle identity for cosine Summary of DoubleAngles • Sine sin 2x = 2 sin x cos x • Cosine cos 2x = cos2 x – sin2 x = 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download
In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometricSin 2x = 2 sin x cos x cos 2x = cos^2 x sin^2 x = 1 2 sin^2 x 2 cos^2 x 1 tan 2x = (2 tan x)/(1 tan^2 x)2tan2 x = sec2 x for values of x in the interval 0 ≤ x < 2π We try to relate the given equation to one of our three identities We can use the identity sec2 x = 1tan2 x to rewrite the equation solely in terms of tanx 2tan2 x = sec2 x 2tan 2x = 1tan x from which tan2 x = 1 Taking the square root then gives tanx = 1 or − 1




Trig Identity Sec2x Minus Tan2x T10 Youtube



Trig Identities Hsn Forum
Prove\\cot (2x)=\frac {1\tan^2 (x)} {2\tan (x)} prove\\csc (2x)=\frac {\sec (x)} {2\sin (x)} prove\\frac {\sin (3x)\sin (7x)} {\cos (3x)\cos (7x)}=\cot (2x) prove\\frac {\csc (\theta)\cot (\theta)} {\tan (\theta)\sin (\theta)}=\cot (\theta)\csc (\theta) prove\\cot (x)\tan (x)=\sec (x)\csc (x) trigonometricidentityprovingcalculator enLet's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ)Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Bestmaths Online Proof 4
Unit 4 Quiz 1 Trig Identities Name_____ ID 1 Date_____ Period____ ©T u2Y0_1U7D NKCuxtVa SBo^f_tCwOaVryeY dLyLlCQE D sAZlZlH BrsitgahmtdsK XreeCsHeirEvreWdh1Verify each identity 1) tan2x sec2x csc2x = sin2x csc2x 2) sec2x (1 csc2x) = csc2x 3) 1 cot2x csc2x The following are the identities of inverse trigonometric functions sin 1 (sin x) = x provided – π /2 ≤ x ≤ π /2 cos 1 (cos x) = x provided 0 ≤ x ≤ π tan 1 (tan x) = x provided – π /2 < x < π /2 sin (sin 1 x) = x provided 1 ≤ x ≤ 1 cos (cos 1 x) = x provided 1 ≤ x ≤ 1 tan (tanList of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) andcos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ andcos θ The tangent (tan) of an angle is the ratio of the sine to the cosine



Derivatives Of Trigonometric Functions




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity
If there are two values of x inside of (), one of the values of x will be denoted as z Learn with flashcards, games, and more — for freeFirstly remember the identities sin^2 x cos^2 x =1 sec^2 x tan^2 x =1 cosec^2 x co t^2 x =1 also remember reciprocal relations cosec x =1 /sin x sec x= 1/cos x cot x =1/tan x and remember the basic algebraic identities (ab)^2 =a^2 b^2 2abC2 Trigonometry Trigonometric Identities PhysicsAndMathsTutorcom Edexcel Internal Review 2 (b) Hence solve, for 0 ≤ x < 360°, the equation 5 cos 2 x = 3(1 sin x), giving your answers to 1 decimal place where appropriate (5) (Total 7 marks) 5 (i) Prove that tan θ cot θ ≡ 2 cosec 2θ, n≠ ∈ n, 2 π θ Z (5)




Tan 2x Formula What Is Tan 2x Formula Examples




Which Of The Following Are Trigonometric Identitie Gauthmath
1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science Tan2x Formula Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved exampleTan(x−y) = (tan x–tan y)/ (1tan x • tan y) Double Angle Identities sin(2x) = 2sin(x) • cos(x) = 2tan x/(1tan 2 x) cos(2x) = cos 2 (x)–sin 2 (x) = (1tan 2 x)/(1tan 2 x) cos(2x) = 2cos 2 (x)−1 = 1–2sin 2 (x) tan(2x) = 2tan(x)/ 1−tan 2 (x) sec (2x) = sec 2 x/(2sec 2 x) csc (2x) = (sec x csc x)/2;
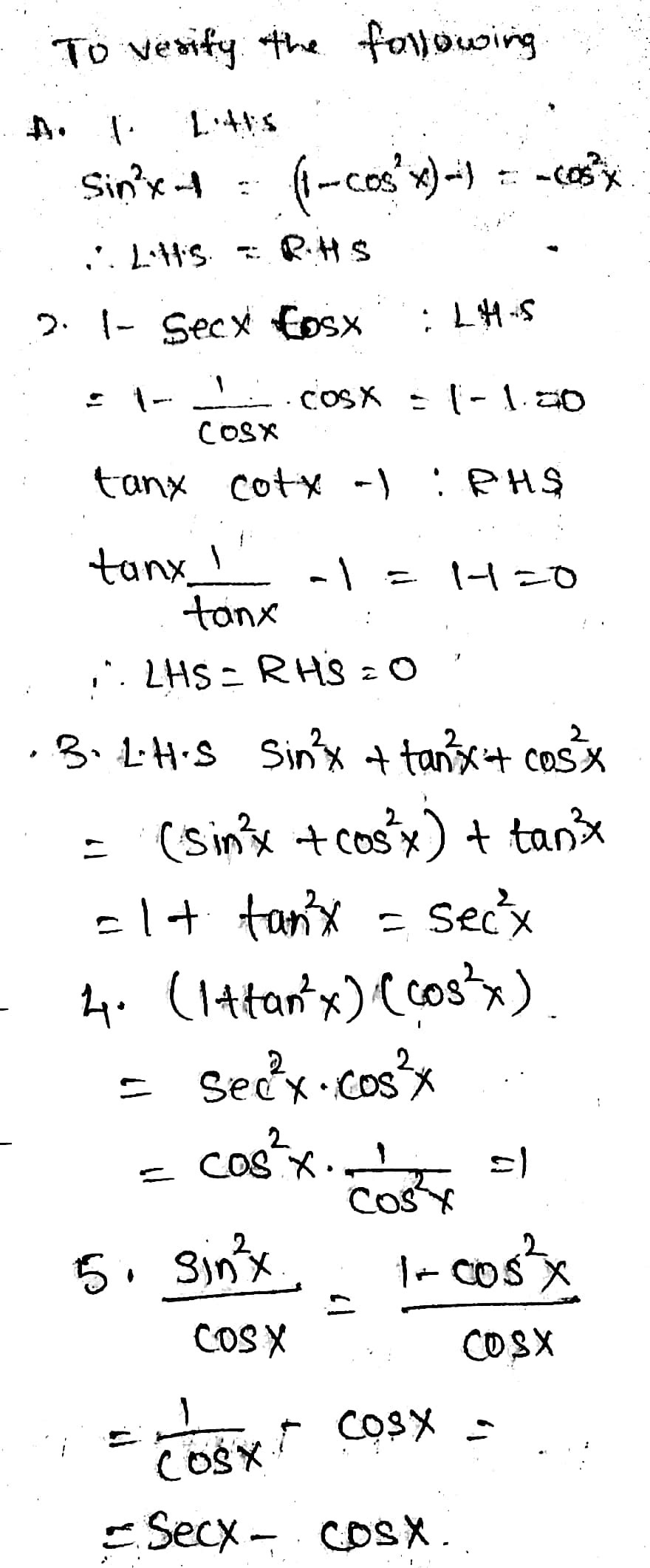



Directions Verify The Following Trigonometric Id Gauthmath




List Of Trigonometric Identities Wikipedia
Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosineSecondly, the identity is tan²θ 1 = sec²θ, not tan²θ 1 Maybe this proof will be easier to follow tan²θ 1 = sin²θ/cos²θ 1 = sin²θ/cos²θ cos²θ/cos²θ = (sin²θ cos²θ)/cos²θ //sin²θ cos²θ = 1, which we substitute in = 1/cos²θ = sec²θ Therefore, tan²θ 1 = sec²θThe basic sumtoproduct identities for sine and cosine are as follows sin x sin y = 2 sin ( x y 2) cos ( x − y 2) cos x cos y = 2 cos ( x y 2) cos ( x − y 2) ) From these identities, we can also infer the differencetoproduct identities




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2




2 Prove The Following Trig Identities A Prove Tan Chegg Com
Basic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian planeAsk for it or check my other videos and playlists!##### PLAYLISTS #####Question Show all steps necessary to verify the trigonometric identity 1tan^2x = csc^2x tan^2x Answer by jsmallt9(3758) (Show Source) You can put this solution on YOUR website!




Math34 Trigonometric Formulas




Integrate Sec 2x Method 1
Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 pFree trigonometric identities list trigonometric identities by request stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy trigonometricidentitycalculator Prove sec^{2}xtan^{2}x=1 enProblem Set 51 Solving Trigonometric Equations With Identities 1 We know g(x) = cosx g ( x) = cos x is an even function, and f (x) =sinx f ( x) = sin x and h(x) = tanx h ( x) = tan x are odd functions




Weierstrass Substitution Wikipedia



Trig Identities Hsn Forum
In this section we look at integrals that involve trig functions In particular we concentrate integrating products of sines and cosines as well as products of secants and tangents We will also briefly look at how to modify the work for products of these trig functions for some quotients of trig functionsTrig identity $1\tan x \tan 2x = \sec 2x$ Ask Question Asked 10 years, 1 month ago Active 5 years, 11 months ago Viewed 6k times 3 0 $\begingroup$ I need to prove that $$1\tan x \tan 2x = \sec 2x$$ I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way everThe trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation cos 2 x − tan 2 x = 2
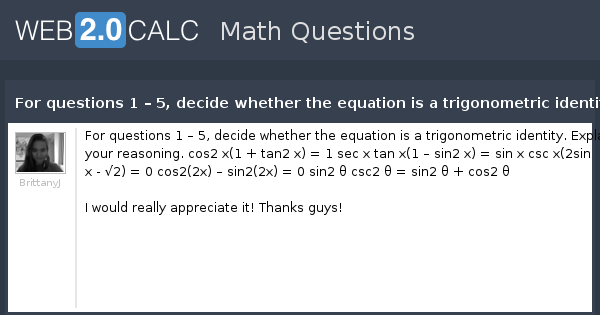



View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning




Sin A B Identity
First of all, please do not try to use fraction bars when you post Most of the time they look so bad they are hard to understand θ = tan − 1(x)isequivalenttox = tanθ sin(sin − 1(x)) = x cos(cos − 1(x)) = x tan(tan − 1(x)) = x sin − 1(sin(θ)) = θ cos − 1(cos(θ)) = θ tan − 1(tan(θ)) = θ Given below are some more inverse trigonometry formulas sin 1 (x) = – sin 1 x



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau



Solved Prove Trigonometric Identities Course Hero




Weierstrass Substitution Wikipedia




Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com



What Is The Formula Of Tan2x Quora




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



1
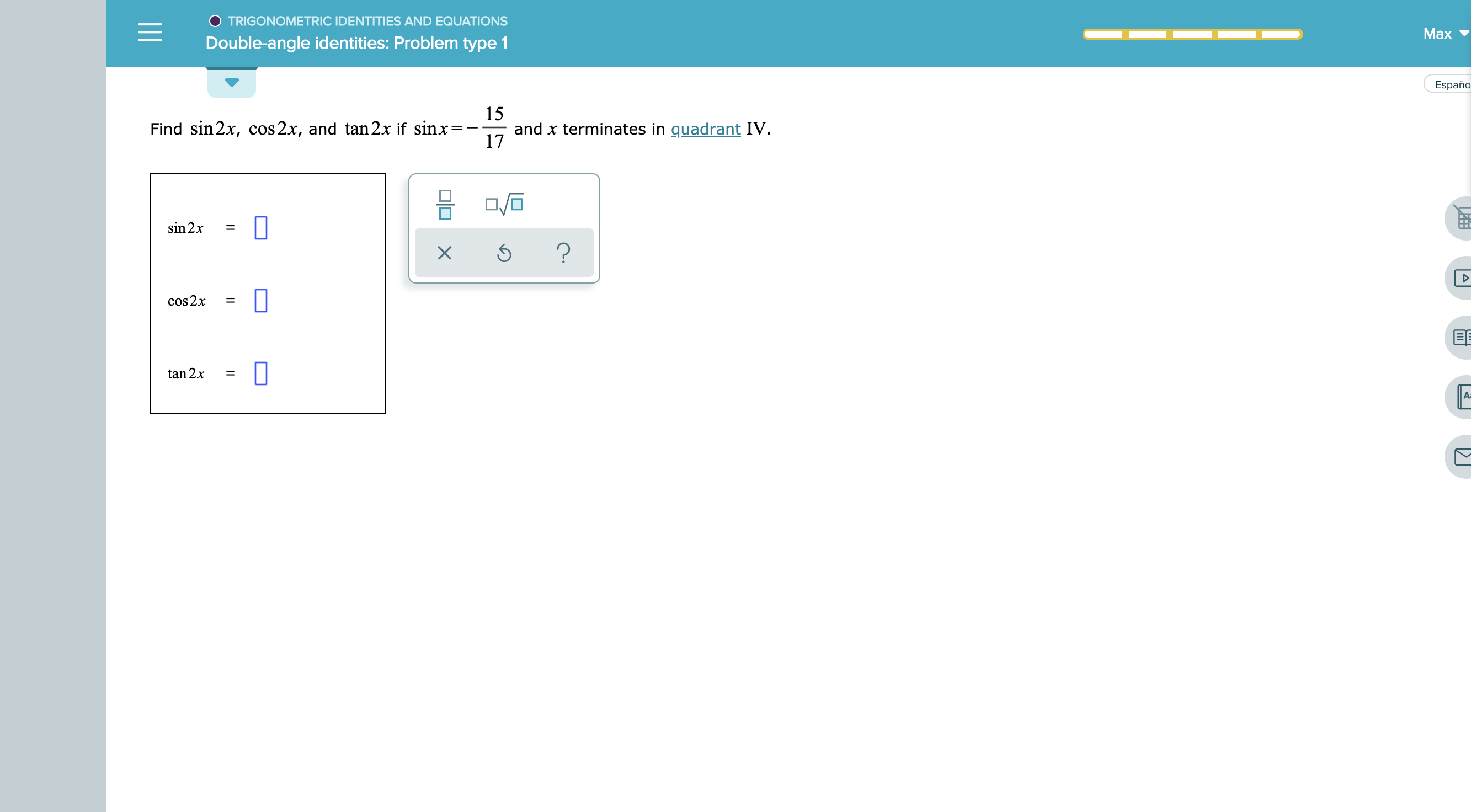



Answered O Trigonometric Identities And Bartleby



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



7 Proving Ids Trig Functions Identities



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




Verify That The Equation Is An Identity Tan 2x Cot Chegg Com




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



3




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians




Sum And Difference Identities Video Lessons Examples And Solutions



Cos2x Identity




List Of Trigonometric Identities Wikipedia




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic




Trig Double Identities Trigonometric Double Angle Functions Trig



Answered O Trigonometric Identities And Bartleby




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




All In One Maths Formula At Your Finger Tips Notes




Chapter 11 Trigonometric Identities And Equations 11 1
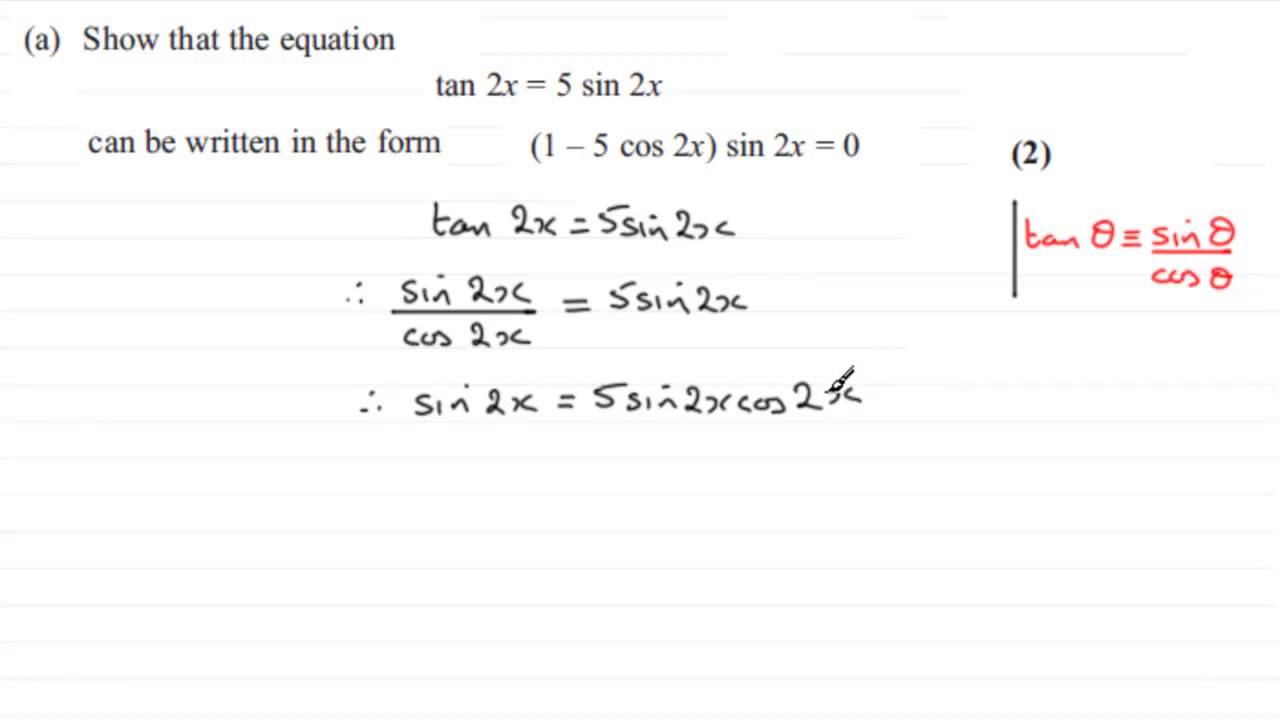



Exam Questions Trigonometric Identities Examsolutions




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Answered O Trigonometric Identities And Bartleby




Inquiry 11 8 Marks Prove The Following Trig Chegg Com




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Cos 2x




Learn Trigonometric Functions Of Multiple Of An Angle In 2 Minutes




Chapter 7 Trigonometric Identities And Equations Ppt Download




Math34 Trigonometric Formulas
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com
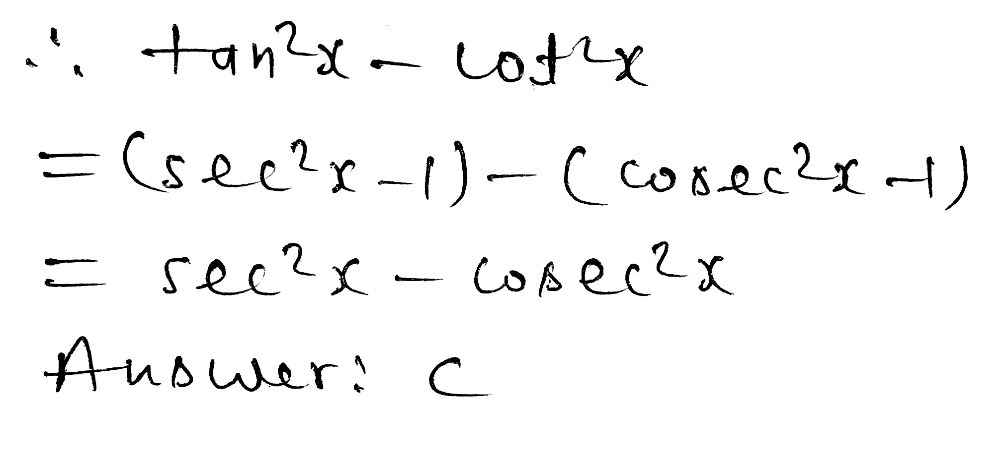



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Trigonometric Identities Trigonometric Functions Trigonometry




Chapter 11 Trigonometric Identities And Equations 11 1
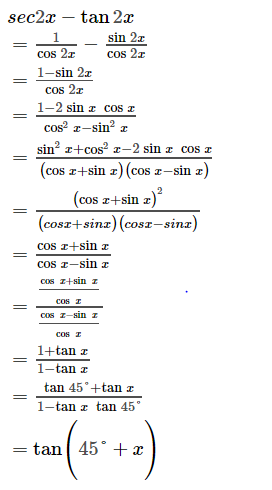



Sec2x Tan2x If0 X P 4




Simplify Each Of The Following Trigonometric Chegg Com
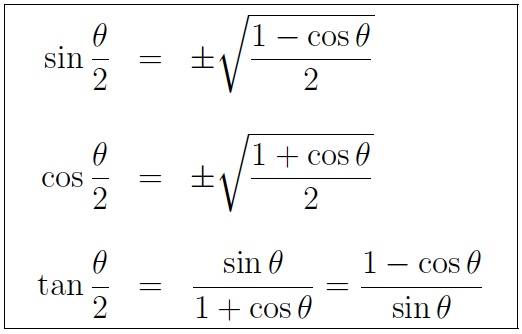



Trig Identities Table Of Trigonometric Identities




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




Tan2x ただの悪魔の画像




9 1 Identities And Proofs Ppt Download




Using Trigonometric Identities Video Khan Academy




Chapter 11 Trigonometric Identities And Equations 11 1




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




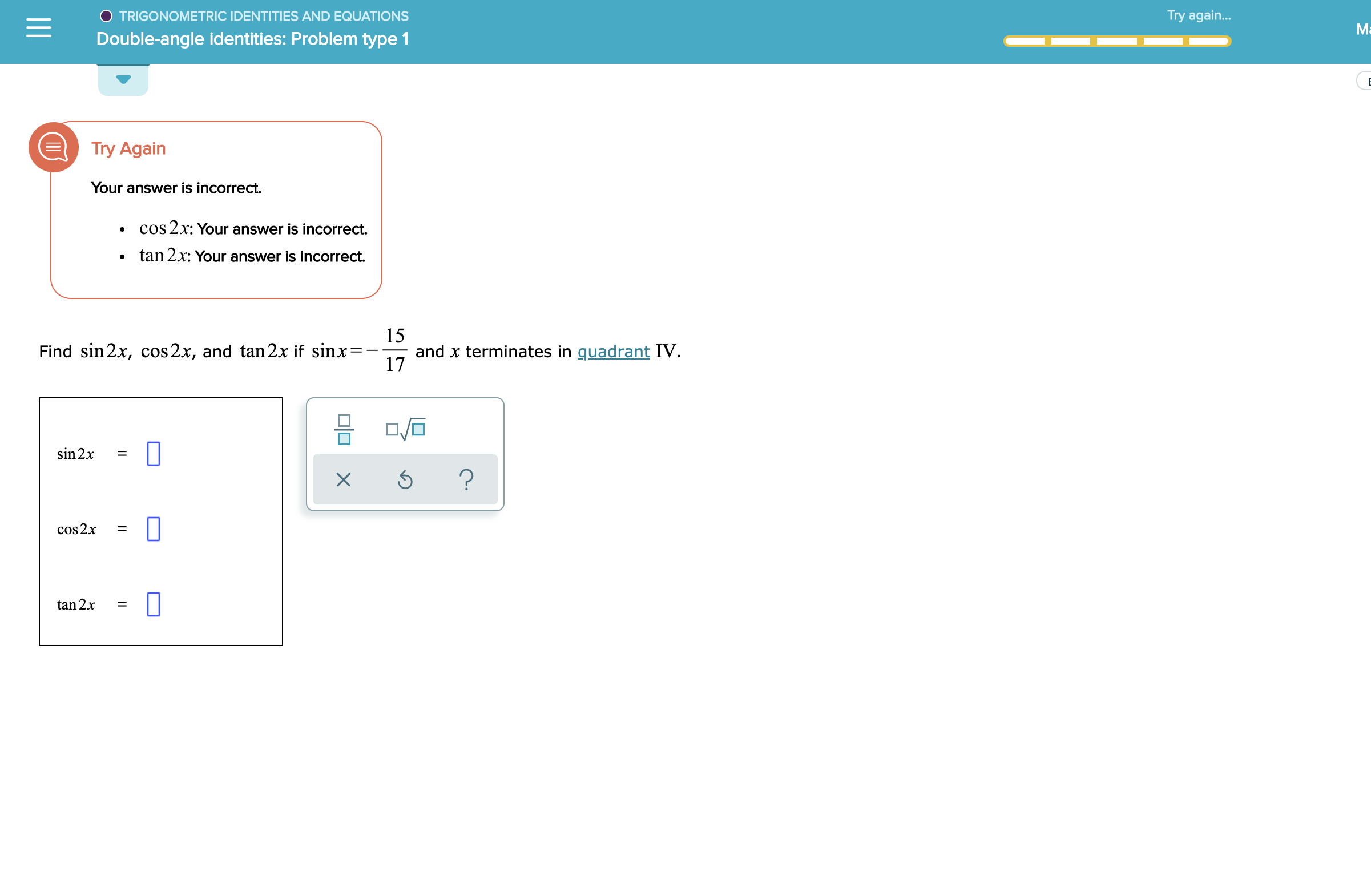
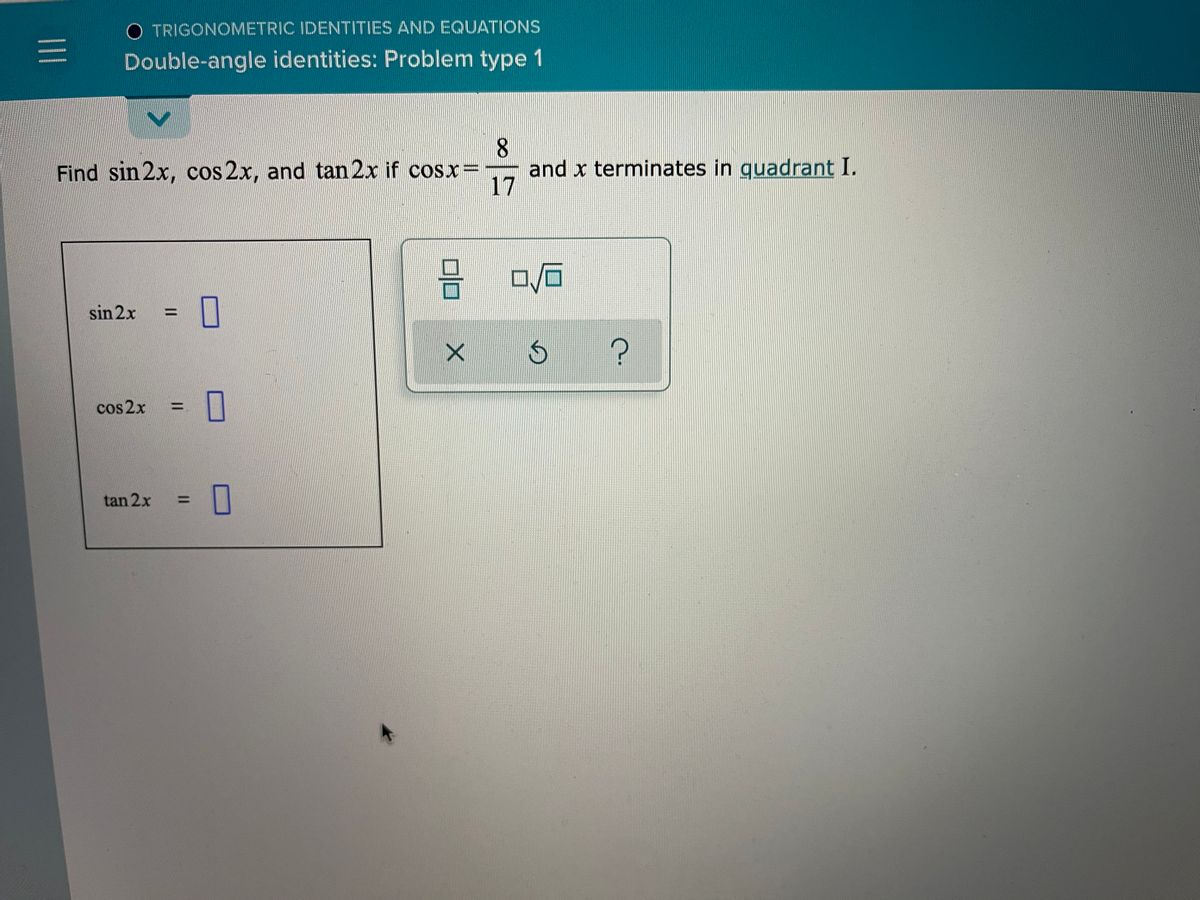
O Trigonometric Identities And Equations Double Angle Identities Problem Type 1 3 Find Sin 2x Cos 2x Homeworklib



Trigonometry Functions User S Blog



What Is The Formula Of Tan2x Quora




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Trig Identities Trigonometric Functions Sine



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



View Question Trig Identities Need Help




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Cos2x Identity




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



1




O Trigonometric Identities And Equations Verifying A Trigonometric Identity Complete The Proof Of The Identity By Homeworklib




Math34 Trigonometric Formulas



Math Problems Simplifying With Trigonometry Identities And Then Integration




Prove The Following Trigonometric Identities Show Gauthmath
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




2 Prove The Following Trig Identities A Prove Tan Chegg Com




Integrate Sec 2x Method 2




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Integrate Tan 2x




Lesson 4 5 Double Angle Formulas




Match The Corresponding Trigonometric Expressions Gauthmath
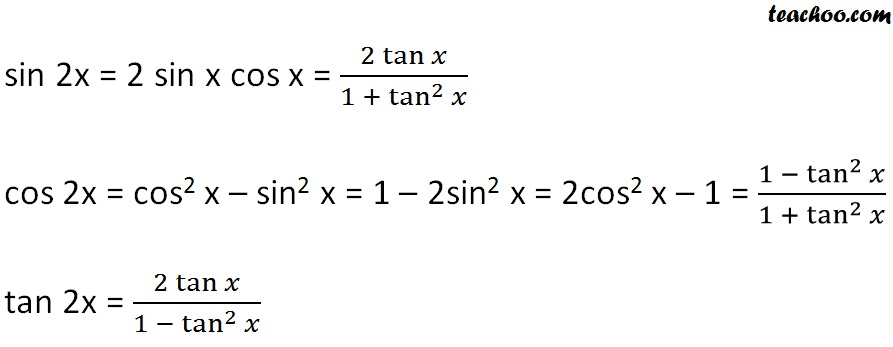



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




Tan2x ただの悪魔の画像




Trig Identities Bingo Card




What Is Integral Of Sin2x Tan2x Quora



0 件のコメント:
コメントを投稿